7./8. Klasse: Kongruenzsätze
1. Teil: Kongruenzsätze
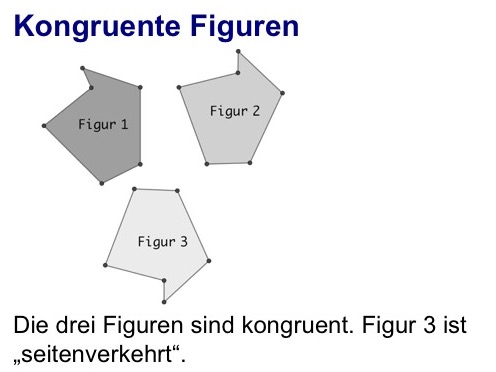
Was bedeutet Kongruenz? Der Begriff wird bereits in der Grundschule als "Deckungsgleichheit" eingeführt und ist sehr anschaulich. Auch seitenverkehrte Figuren können kongruent sein.
Audio file
Warum wird das Thema im Unterricht behandelt? Es handelt sich um ein Musterbeispiel für mathematisches Arbeiten, das eben mehr ist als Aufgaben "rechnen".
Audio file

Hier geht es um die Frage, wie viele Angaben nötig sind, um ein Dreieck eindeutig konstruieren zu können. Das könnte man theoretisch klären, hier geht es aber eher um einen experimentellen Zugang. Aus Dreiecken kann man alle ebenen Figuren zusammensetzen, deshalb ist die Dreieckslehre so fundamental.
Audio file
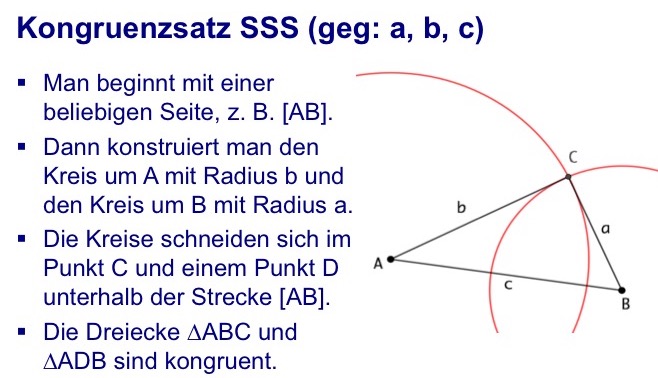
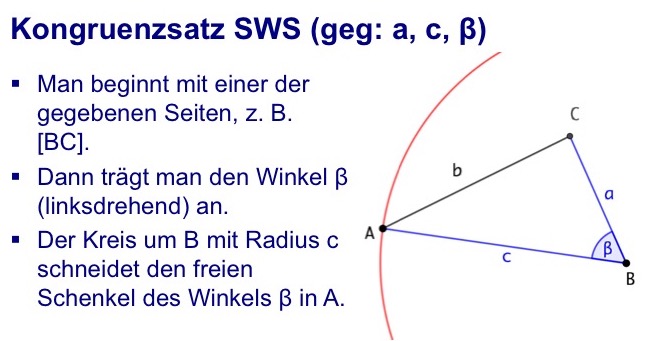
Es gibt vier verschiedene Möglichkeiten, drei Angaben (Seiten - Winkel) zu machen. Für jede Möglichkeit sind in den Bildern und Texten Beispiele vorgeführt.
Audio file

Wenn Sie das Wort Link anklicken, können Sie selbst experimentieren. Verziehen Sie den Punkt P mit der Maus und beobachten Sie, unter welcher Bedingung ein eindeutiger Schnittpunkt zwischen Kreis und freiem Schenkel des Winkels entsteht.
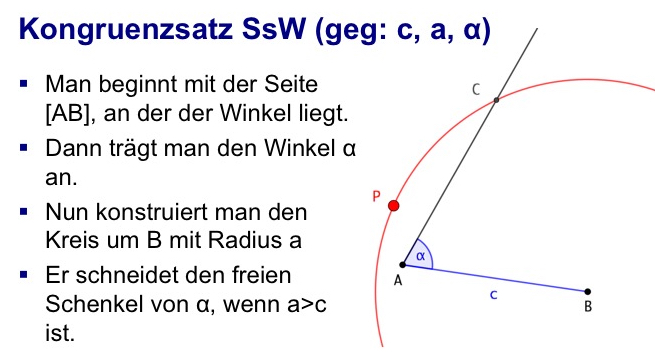
Ist der Kreisradius kleiner als c, dann gibt es keinen Schnittpunkt oder zwei Schnittpunkte, also keine eindeutige Lösung. Ist der Kreisradius größer als c, dann gibt es genau eine Lösung.
Um anzudeuten, dass der Kongruenzsatz gilt, wenn der gegebene Winkel der längeren Seite gegenüberliegt, schreibt man SsW oder SSWg.
Geht es um die Konstruktion eines Vierecks hilft es in den meisten Fällen, in der Überlegungsfigur eine Diagonale einzuzeichnen. Dadurch erhält man zwei (Teil-)Dreiecke. In einem sollten die Angaben einem Kongruenzsatz entsprechen. Dieses ist deshalb eindeutig konstruierbar.
2. Teil: Kongruenzbeweise
Man kann beim Beweisen lernen, sachlich und folgerichtig zu argumentieren. Deshalb ist Beweisen auch in der Schule wichtig.
Audio file
Ein Dreieck mit zwei gleich langen Seiten hat auch zwei gleich große Winkel.
Audio file
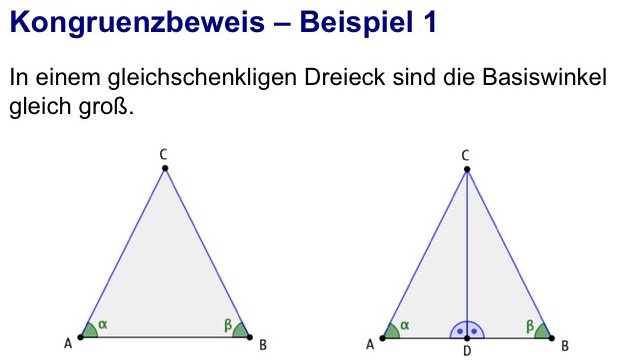
Ein Beweis hat drei Teile: Voraussetzung, Behauptung und folgerichtige Argumentation.
Im Beispiel ist vorausgesetzt, dass das Dreieck ABC gleichschenklig ist. Als Hilfslinie ist die Höhe [DC] eingetragen.
Audio file

Ein zweites Beispiel zu gleichschenkligen Dreiecken.
Voraussetzung ist, dass das Dreieck ABC gleichschenklig ist und die Winkel 𝛅 und 𝛆 bei C gleich groß sind.
Audio file
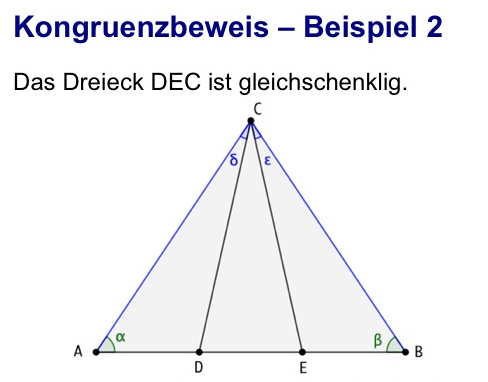
Die Dreiecke ADC und BEC sind wegen WSW kongruent.
