7. Klasse: Variable und Gleichungen
1. Teil: Variable
Was ist denn eine Variable? x, y? Variable stehen immer für Zahlen. Eine Variable kann eine feste Zahl sein. Sie kann aber auch viele verschiedene Zahlen vertreten.
Variable können als Platzhalter für eine feste, meist unbekannte Zahl dienen. Man sagt deshalb auch "Unbekannte".
Audio file

Variablen können auch für viele verschiedene Zahlen stehen. Man sagt manchmal auch "Veränderliche".
Audio file
Der Variablenbegriff wird in höheren Klassen noch erweitert.
2. Teil: Gleichungen
Das Gleichheitszeichen "=" kann mehrere Bedeutungen haben. Zunächst steht es zwischen einer Aufgabe und ihrem (Rechen-) Ergebnis. Es hat aber noch weit größere Bedeutung:
Audio file

Zur Aufgabe-Ergebnis-Deutung (Ausrechnen) kommt die algebraische Sichtweise (Wertgleichheit).
Audio file

Audio file

3. Teil: Lösen einfacher Gleichungen
Gleichungen lösen? Das ist ganz einfach! Dafür gibt´s doch ein Schema F …
So einfach ist das nicht. Das Verständnis muss schrittweise aufgebaut werden. Wie, das hören und sehen Sie hier.
Audio file

Das Thema Gleichungslösen wird im Unterricht häufig mit Zahlenrätseln begonnen. Die Idee ist, eine gemerkte Zahl so in eine Rechnung einzubauen, dass sie gewissermaßen "versteckt" oder "eingepackt" ist. Das Rätsel ist gelöst, wenn die Zahl gefunden bzw. "ausgepackt" ist.
Audio file

Beim Einpacken wird in diesem einfachen Beispiel zuerst mit 7 multipliziert und dann vom Ergebnis 12 subtrahiert (obere Zeile). Auspacken bedeutet, diese Rechenschritte der Reihe nach rückgängig zu machen (untere Zeile).
Audio file
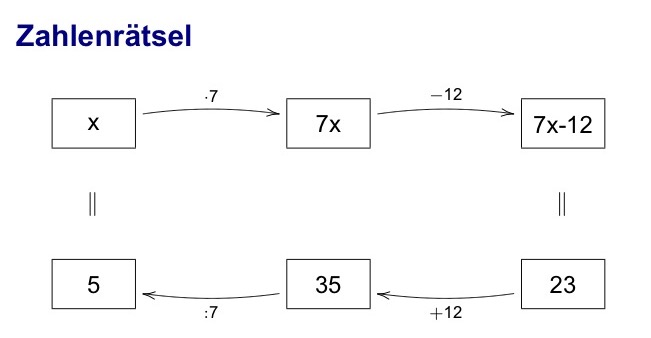
Die Darstellung im Boxenmodell bereitet auf das allgemeine Lösungsverfahren mit "Äquivalenzumformungen" vor. Die Boxen stehen für die Variable und die Hölzchen für die Zahl 1. Drei Boxen bedeuten also 3x und 2 Hölzchen die Zahl 2.
Audio file
Video file
Nicht alle Gleichungen kann man im Boxenmodell darstellen. Die Vorgehensweise funktioniert aber auch für andere Fälle. Die Idee ist, Operationen auf beiden Seiten der Gleichung durchzuführen, die die Lösung nicht verändern.
Audio file

Im Beispiel wird das Verfahren "Gleichungslösen mit Äquivalenzumformungen" vorgeführt.
Audio file

Nicht alle Operationen sind Äquvalenzumformungen. Insbesondere, wenn man die beiden Seiten der Gleichung mit einem Term multipliziert, der die Variable enthält, kann man Ergebnisse erhalten, die keine Lösungen der Gleichung sind. Dividiert man durch einen Term, der die Variable enthält, können Lösungen "verloren" gehen.
Audio file